Probability and Statistics

Investment decisions are based on future events. If we could foretell future, our decisions would be obvious. But as we know, this is not possible and we are faced with uncertainty. To deal with uncertainty we use probability and statistics.

Probability is a quantitative measure of uncertainty. Statistics deals with collecting, analyzing, interpreting and presenting numerical data. Part of its purpose is to summarize what has happened in order to predict what will happen or what might happen. In this way statistics is closely connected with probability, which is the science of predicting the likelihood of events.

For example, If we flip the coin, the probability of getting head is 0.5. This means that, if we toss the coin many times, we expect heads in about 50% of the flips. Probability is a number between 0 and 1. Zero implies the event cannot occur and 1 means that it is absolutely certain to happen. If an event is as likely to occur as not occur, the probability of event occurring is 0.5. There are many methods of calculating probabilities, the simplest ones are based on ratios. The underlying assumption of these methods is the idea that what is probable depends on what is possible. If an experiment (tossing a coin, picking a card from a deck, etc.) has a set of distinct outcomes, each of which is equally likely to occur, then the probability of an event is the ratio of the number of outcomes that constitute the event (getting head, picking diamond, etc.) to the total number of possible outcomes:

P(event) = (number of event outcomes ) / (number of total outcomes).

In case of tossing coin, the probability of getting the head is:

P(head) = 1/2 = 0.5.

Random Variables

Future returns of investment are uncertain. If probabilities can be assigned to all possible return outcomes, than the return is an example of a random variable. Random variable is a variable that takes numerical values determined by chance. It may be discrete or continuous. The discrete variable assumes countable number of values, continuous variable may take on any value in an interval of numbers. If we assign probabilities to each numerical value we get what is called probability distribution of the random variable.

Stock rate of return can be considered as a random variable because of uncertainty involved. Based on our predictions of certain events occurring we can formulate a probability distribution of rate of return. Probabilities can be derived from our beliefs, mathematical model, financial analysts recommendation, etc.
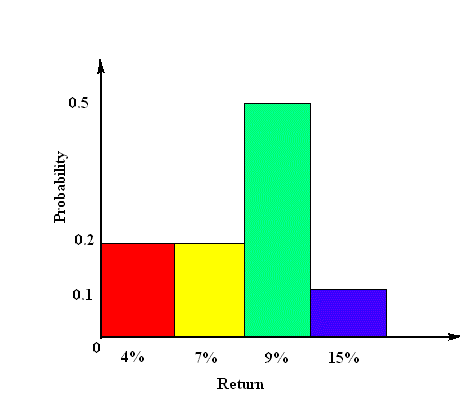
For example, for hypothetical stock S:

   		   			Rate of return:		    Probability:
			 	    	    4%				0.2
				    	    7%				0.2
				    	    9%				0.5
				   	    15%				0.1
									----
									1.0

The events of probability distribution represent outcomes that are mutually exclusive and collectively exhaustive. This means that only one of the events must take place and sum of probabilities will equal 1.

Expected Value

It is difficult to compare different investment opportunities by looking at their probability distributions. An investor needs a single measure that encapsulates or summarizes investment returns and corresponding probabilities and gives clear parameter for comparing different securities or portfolios. The central tendency is the most intuitive characteristic of the probability distribution. The expected value or mean is one of the measures of central tendency. It is computed by taking the weighted average of different outcomes of the random variable where weights are the probabilities:

Expected Value(V) = a*P(a) + b*P(b) + c*P(c) + ... ,

where a, b, c, ... are different outcomes and P(a), P(b), P(c), ... are corresponding probabilities of random variable V. For above numerical example of stock S the expected value equals:

Expected Value(S) = 4%*0.2 + 7%*0.2 + 9%*0.5 + 15%*0.1 = 8.2%.

The expected value can be interpreted as a long run average, or in other words, if many outcomes of the random variable can be observed, we would "expect" the average of this outcomes to be approximately equal to the expected value. Other measures of central tendency are mode and median. The mode is the value that is most likely to occur. The median is the value where the random variable is equally likely to occur above it as below it. Although any of these three measures can be used in security analysis, expected value (mean) is the most preferred. The reason is that both, the values and their associated probabilities of the random variable are used in mean calculation and any changes in values and probabilities are reflected in mean.

Standard Deviation and Variance

The central tendency measures (mean, median, mode) do not reflect very important characteristic of investment, which is risk. The probability distribution variability is used to quantify the risk. The variability is measured by variance and standard deviation. The variance is a weighted sum of squares of deviations of outcomes from expected value, where weights are corresponding probabilities of the outcomes:

Variance(V) = (sq(a-X))*P(a) + (sq(b-X))*P(b) + (sq(c-X))*P(c) +... ,

where a, b, c, ... are different outcomes of random variable V, P(a), P(b), P(c), ... are corresponding probabilities, X is expected value (mean) and "sq" means square. The standard deviation is a square root from variance value:

Standard Deviation(V) = sqrt( Variance(V) ),

where "sqrt" means square root.
For above numerical example of stock S the variance and standard deviation equals:

	Variance(S) = sq(4-8.2)*0.2 + sq(7-8.2)*0.2 + sq(9-8.2)*0.5 + sq(15-8.2)*0.1 = 
            	    = sq(-4.2) *0.2 +  sq(-1.2)*0.2 +  sq(0.8 )*0.5 +    sq(6.8)*0.1 = 
                    =     17.64*0.2 +      1.44*0.2 +      0.64*0.5 +      46.24*0.1 =
                    =	      3.528 +         0.288 +          0.32 +          4.624 =
                    = 8.76

	Standard Deviation(S) = sqrt( 8.76 ) = 2.96%

Since the variance and standard deviation quantify how far return values lie from the expected return value, they are used as a measure of risk for investment.