Derivatives

A Derivative is a financial instrument whose value depends on the values of other, more basic underlying variables. Very often the variables underlying derivatives are the prices of traded securities. A stock option, for example, is a derivative whose value is dependent on the price of a stock. However, derivatives can be dependant on almost any variable, from price of oil to amount of snow falling at a certain place. Examples of derivatives are forward contracts, futures, options, swaps, etc

Forwards and Futures

A forward contract is an agreement to buy or sell a security at a certain future time for a certain price. The buyer of the forward agrees to pay the price and take delivery of the good or instrument and is said to be long the forward, while the seller of the forward, or short, agrees to deliver the good or instrument at the agreed price on the agreed date. The forwards are not normally traded on exchange. Forwards with certain standardized (by exchange) features are called futures. Futures are traded on exchange.

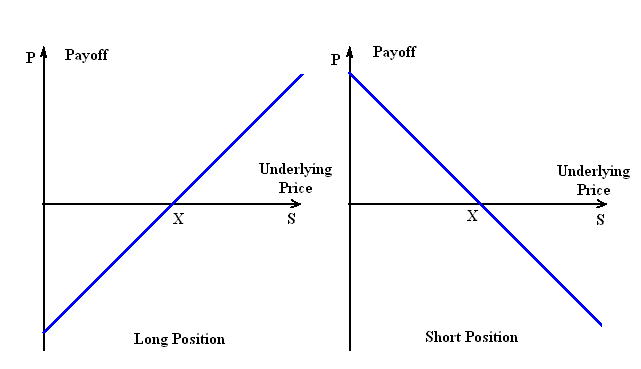
The price specified in forward contract is called delivery price or price at maturity. A forward contract is settled at maturity, when the holder of short position delivers the security to the holder of the long position in return for cash amount equal to the delivery price. The value of forward contract is determined by the market price of the underlying security. The forward price is defined as the delivery price which would make the forward contract to have zero value. It follows that the forward and delivery prices are equal at the time the contract entered into and it costs nothing to take either a long or a short position. As time passes the underlying security price changes which entails the change of forward contract value(price).

The payoff from a long position in a forward contract is

P = S - X ,

where S is a spot price of the security at time of contract maturity, X is the delivery price. Similarly, the payoff from a short position is

P = X - S .

For example, let's say the current price of the stock is $80.00 and we entered in forward contract to buy this stock in 3 months time for $81.00 (that means we hope that price will not fall lower than $81.00). If after three months price is more than $81.00, let's say $83.00, than we can buy the same stock for $81.00 (as stated by forward contract) and after reselling it on the market our payoff will be

P = $83.00 - $81.00 = $2.00

If at forward maturity the stock price falls to $78.00, than our loss will be

P = $81.00 - $78.00 = $3.00

The graphs above illustrate the forward contract payoff patterns for long and short positions.

Options

An option is a stipulated privilege of buying or selling a stated security, commodity, or property at a given price (called strike price) within a specified time. There are two basic types of options. A call option gives the holder the right to buy the underlying security by a certain date for a certain price. A put option gives the holder right to sell the underlying security by a certain date for a certain price. The date in the contract is called exercise date, expiration date or maturity. American options can be exercised at any time up to the expiration date. European options can be exercised only on the expiration date.

The important point to emphesize is that an option gives the holder the right to do something but the holder doesn't have to exercise this right. This distinguishes options from forwards and futures, where the holder is obligated to buy or sell the underlying security.

If S is a final price of the option underlying security, X is a strike price and OP is an option price, than the profit is

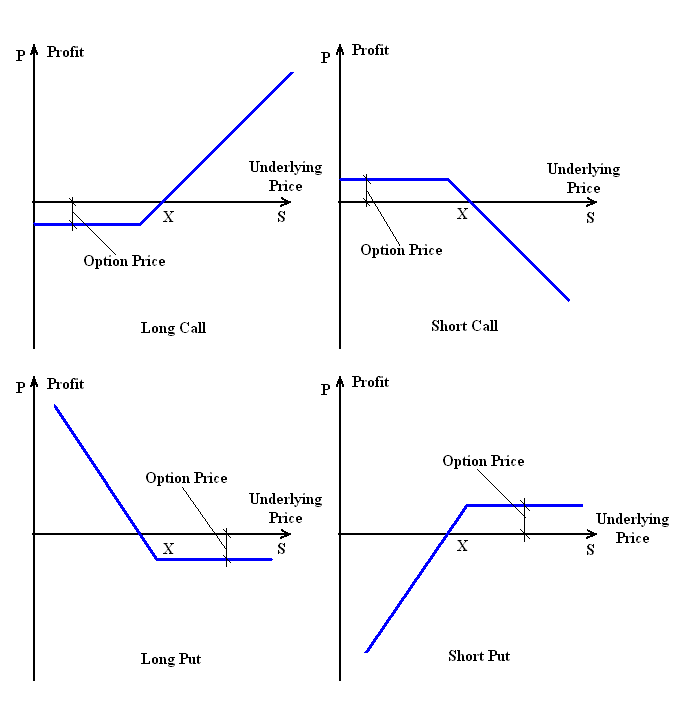
						Long  Call:  P = S - X - OP
						Short Call:  P = X - S + OP
						Long  Put:   P = X - S - OP
						Short Put:   P = S - X + OP

For example, let's say the stock price is $50.00, we bought European call option with strike $53.00 and paid $2.00 for this option. If option price is less than $53.00, we will not exercise the option to buy the stock, because it doesn't make sense to buy security for higher price than it costs on the market. In this case we lose all initial investment equal to the option price $2.00. If stock price is more than $53.00, we will exercise the option. For example if the stock price is $56.00, after exercising the option and immediately reselling the acquired stock our profit will be:

P = $56.00 - $53.00 - $2.00 = $1.00

if the stock price is $54.00, than the profit is:

P = $54.00 - $53.00 - $2.00 = - $1.00

As we see in latter case we lose money. The reason is that increase of stock price just by $1.00 above the strike ($53.00) doesn't cover our initial investment of $2.00, although we still exercise the option to recover at least $1.00 of initial investment. If the stock price at exercise time is $55.00 than we exercise the option to cover our initial expenses(equal to option price):

P = $55.00 - $53.00 - $2.00 = $0.00

This latter case corresponds to option graph intersection point with horizontal axis on the drawing above.